
Cálculo de vetores de equilíbrio, exemplos, exercícios
O vetor de equilíbrio É aquele que se opõe ao vetor resultante e, portanto, é capaz de balancear um sistema, uma vez que possui a mesma magnitude e mesmo sentido, mas sentido contrário a este..
Em muitas ocasiões, o vetor de equilíbrio se refere a um vetor de força. Para calcular a força de equilíbrio, primeiro encontre a força resultante, conforme mostrado na figura a seguir:
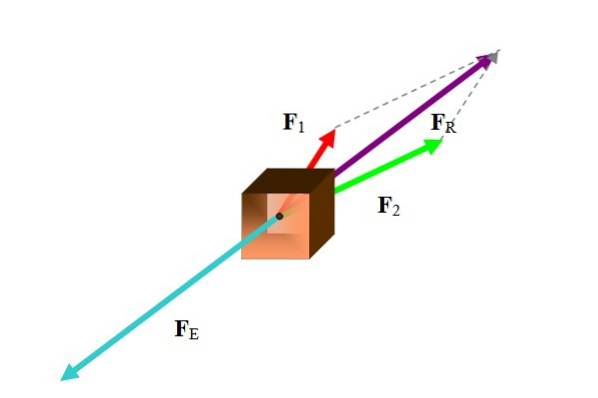
Existem vários métodos para realizar essa tarefa, dependendo dos dados disponíveis. Uma vez que as forças são vetores, a resultante é a soma vetorial das forças participantes:
FR = F1 + Fdois + F3 + ... .
Entre os métodos a serem utilizados estão métodos gráficos como poligonal, paralelogramo e métodos analíticos como decomposição de forças em seus componentes cartesianos. No exemplo, a figura usou o método de paralelogramo.
Uma vez que a força resultante foi encontrada, a força de equilíbrio é apenas o vetor oposto.
sim FE é a força de equilíbrio, então fica satisfeito que FE aplicado em um determinado ponto, garante o equilíbrio translacional do sistema. Se for uma única partícula, ela não se moverá (ou talvez se mova com velocidade constante), mas se for um objeto estendido, ainda terá a capacidade de girar:
FR + FE = 0
Índice do artigo
- 1 exemplos
- 1.1 Tabela de força
- 2 exercícios resolvidos
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Exemplos
As forças de equilíbrio estão presentes em todos os lugares. Nós mesmos somos equilibrados pela força que a cadeira exerce para compensar o peso. Os objetos que estão em repouso: livros, móveis, lâmpadas de teto e um grande número de mecanismos, estão continuamente sendo equilibrados por forças.
Por exemplo, um livro em repouso sobre uma mesa é equilibrado pela força normal que exerce sobre o livro, impedindo-o de cair. O mesmo acontece com a corrente ou cabo que segura a lâmpada pendurada no teto em uma sala. Os cabos que sustentam uma carga distribuem seu peso por meio da tensão neles.
Em um fluido, alguns objetos são capazes de flutuar e permanecer em repouso, uma vez que seu peso é equilibrado por uma força ascendente exercida pelo líquido, chamada Empurre.
Vários mecanismos precisam ser equilibrados, conhecendo o vetor de força de equilíbrio, como barras, vigas e colunas.
Ao usar uma balança, é necessário equilibrar de alguma forma o peso do objeto com uma força equivalente, seja somando pesos ou por meio de molas..
Tabela de força
A tabela de força é usada em laboratório para determinar a força de equilíbrio. Consiste em uma plataforma circular, da qual você tem a vista de cima na figura, e que possui um transferidor para medir ângulos.
Nas bordas da mesa existem roldanas por onde passam as cordas que seguram os pesos e que convergem em um anel que fica no centro.
Por exemplo, dois pesos são pendurados. As tensões geradas nas cordas por esses pesos são desenhadas em vermelho e azul na figura 2. Um terceiro peso em verde pode equilibrar a força resultante dos outros dois e manter o sistema em equilíbrio..
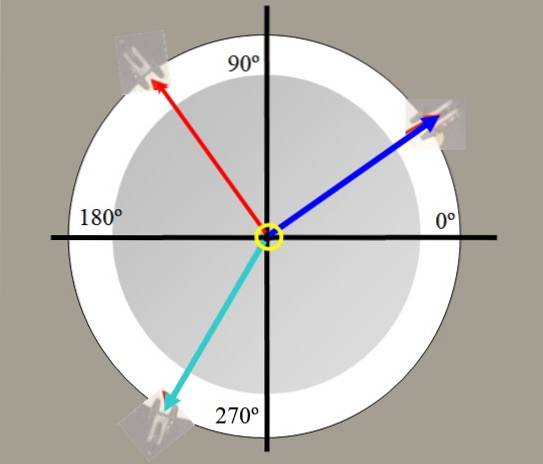
Com a tabela de forças é possível verificar o caráter vetorial das forças, decompor as forças, encontrar a força de equilíbrio e verificar o teorema de Lamy:
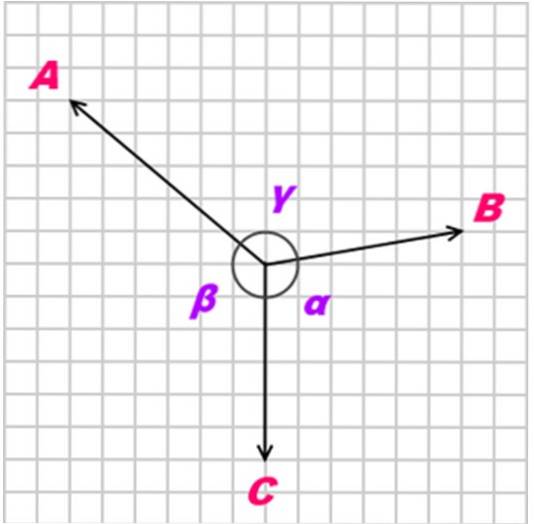
Sim um corpo está em equilíbrio graças a três forças coplanares, concorrentes e não colineares (não paralelas), chamadas PARA, B Y C, a relação entre essas forças é a seguinte:
A / sin α = B / sin β = C / sin γ
Exercícios resolvidos
-Exercício 1
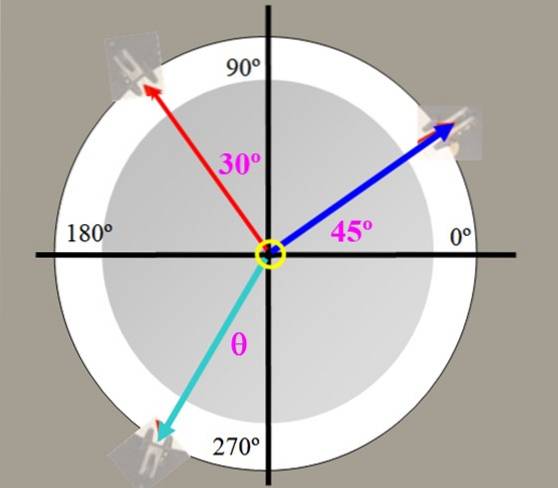
Pesos de 225 g (tensão azul) e 150 g (tensão vermelha) são pendurados na mesa de força da Figura 2, com os ângulos mostrados. Encontre o valor da força de equilíbrio e o ângulo que ela faz com o eixo vertical.
Solução
O problema pode ser trabalhado com os pesos expressos em gramas (forças). Deixe P1 = 150 gramas e Pdois = 225 gramas, os respectivos componentes de cada um são:
P1x = 225. cos 45 ° g = 159,10 g; P1a = 225. cos 45º g = 159,10 g
P2x = -150. sen 30 g = -75,00 g; P2 e = 150. cos 30º g = 129,90 g
O peso resultante PR é encontrado adicionando algebricamente os componentes:
PRx = 159,10 - 75,00 g = 84,10 g
PRy = 159,10 + 129,90 g = 289,00 g
O peso de equilíbrio PE é o vetor oposto PR:
PAntigo = -84,10 g
PEi = -289,00 g
A magnitude do peso de equilíbrio é calculada por:
PE = (PAntigodois + PEidois)1/2 = ((-84,10)dois + (-289,00)dois)1/2 g = 301 g
O ângulo θ na figura é:
θ = arctg (-84,10 / -289,00) = 16,2º em relação ao eixo Y negativo.
-Exercício 2
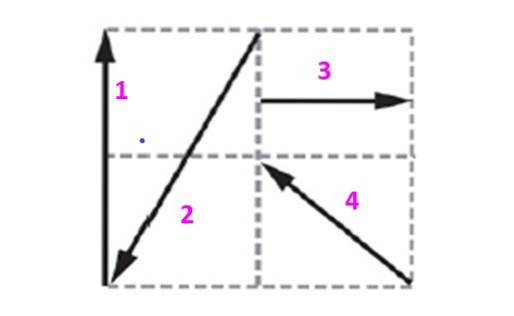
Encontre o vetor de equilíbrio do sistema mostrado na figura, sabendo que cada quadrado mede 10 m de lado.
Solução
Os vetores contidos nesta grade serão expressos em termos de vetores unitários e ortogonais eu Y j que determinam o plano. Vetor 1, que será denotado como v1 tem magnitude de 20 me é direcionado verticalmente para cima. Pode ser expresso como:
v1 = 0 eu +vinte j m
No desenho, pode-se ver que o vetor 2 é:
vdois = -10 eu - vinte j m
O vetor 3 é horizontal e aponta na direção positiva:
v3 = 10 eu + 0 j m
Finalmente o vetor 4 está inclinado 45º, pois é a diagonal do quadrado, portanto seus componentes medem os mesmos:
v4 = -10 eu + 10 j m
Observe que os sinais indicam em que lado do eixo os componentes estão: acima e à direita têm um sinal +, enquanto abaixo e à esquerda eles têm um sinal -.
O vetor resultante é obtido adicionando componente a componente:
vR = -10 eu + 10 j m
Então, o vetor de equilíbrio do sistema é:
vE = 10 eu - 10 j m
Referências
- Beardon, T. 2011. Uma introdução aos vetores. Obtido em: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Série: Física para Ciências e Engenharia. Volume 1. Cinemática. 31-68.
- Fisica. Módulo 8: Vetores. Recuperado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecânica para Engenheiros. Estático. 6ª Edição. Editora Continental. 15-53.
- Calculadora de adição de vetor. Recuperado de: 1728.org
- Vetores. Recuperado de: wikibooks.org



Ainda sem comentários