
Definição de vetores não coplanares, condições, exercícios
O vetores não coplanares são aqueles que não compartilham o mesmo plano. Dois vetores livres e um ponto definem um único plano. Um terceiro vetor pode ou não compartilhar esse plano e se não compartilhar, eles são vetores não coplanares.
Os vetores não coplanares não podem ser representados em espaços bidimensionais como um quadro negro ou uma folha de papel, porque alguns deles estão contidos na terceira dimensão. Para representá-los adequadamente, você deve usar a perspectiva.
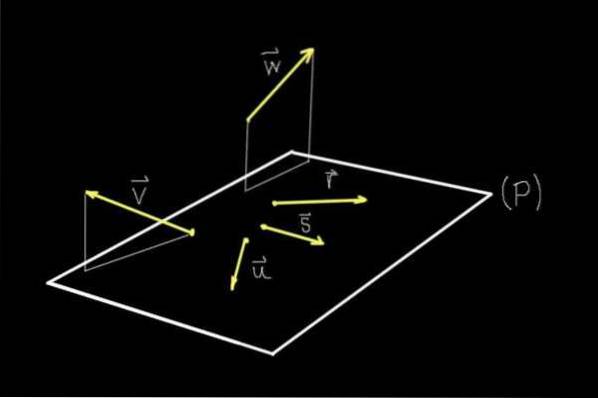
Se olharmos para a figura 1, todos os objetos mostrados estão estritamente no plano da tela, porém graças à perspectiva nosso cérebro é capaz de imaginar um plano (P) que sai dela..
Nesse plano (P) estão os vetores r, s, ou, enquanto os vetores v Y C eles não estão naquele avião.
Portanto, os vetores r, s, ou eles são coplanares ou coplanares entre si, uma vez que compartilham o mesmo plano (P). Vetores v Y C eles não compartilham um plano com nenhum dos outros vetores mostrados, portanto, eles são não coplanares.
Índice do artigo
- 1 Vetores coplanares e equação do plano
- 1.1 Equação cartesiana do plano
- 2 Condições para três vetores serem não coplanares
- 2.1 Condição de não coplanaridade
- 2.2 Condição alternativa de não coplanaridade
- 3 exercícios resolvidos
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
Vetores coplanares e equação do plano
Um plano é definido exclusivamente se três pontos ocorrerem no espaço tridimensional.
Suponha que esses três pontos sejam o ponto PARA, o ponto B e o ponto C que definem o plano (P). Com esses pontos é possível construir dois vetores AB = u Y AC = v que são por construção coplanares com o plano (P).
O produto vetorial (ou produto vetorial) desses dois vetores resulta em um terceiro vetor perpendicular (ou normal) a eles e, portanto, perpendicular ao plano (P):
n = u X v => n ⊥ ou Y n ⊥ v => n ⊥ (P)
Qualquer outro ponto que pertença ao avião (P) deve satisfazer que o vetor AQ é perpendicular ao vetor n; Isso é equivalente a dizer que o produto escalar (ou produto escalar) de n com AQ deve ser zero:
n • AQ = 0 (*)
A condição anterior é equivalente a dizer que:
AQ • (ou X v) = 0
Esta equação garante que o ponto Q pertence ao avião (P).
Equação cartesiana do plano
A equação acima pode ser escrita na forma cartesiana. Para isso, escrevemos as coordenadas dos pontos PARA, Q e os componentes do vetor normal n:
A = (a, b, c)
Q = (x, y, z)
n= (nx, ny, nz)
Portanto, os componentes do AQ são:
AQ= (x-a, y-b, z-c)
A condição para o vetor AQ está contido no avião (P) é a condição (*) que agora está escrita assim:
(nx, ny, nz) • (x-a, y-b, z-c) = 0
O cálculo do produto escalar permanece:
nx (x-a) + ny (y-b) + nz (z-b) = 0
Se for desenvolvido e reorganizado, permanece:
nx x + ny y + nz z = nx a + ny b + nz c
A expressão anterior é a equação cartesiana de um plano (P), como uma função dos componentes de um vetor normal para (P) e as coordenadas de um ponto PARA que pertence a (P).
Condições para três vetores serem não coplanares
Como visto na seção anterior, a condição AQ • (ou X v) = 0 garante que o vetor AQ é coplanar com ou Y v.
Se ligarmos C para vetor AQ então podemos afirmar que:
C, ou Y v eles são coplanares, se e somente se C • ( ou X v ) = 0.
Condição de não coplanaridade
Se o produto triplo (ou produto misto) de três vetores for diferente de zero, então esses três vetores são não coplanares.
sim C • ( ou X v ) ≠ 0 então os vetores u, v e w são não coplanares.
Se os componentes cartesianos dos vetores u, v e w forem introduzidos, a condição de não coplanaridade pode ser escrita assim:
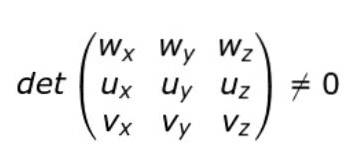
O triplo produto tem uma interpretação geométrica e representa o volume do paralelepípedo gerado pelos três vetores não coplanares..
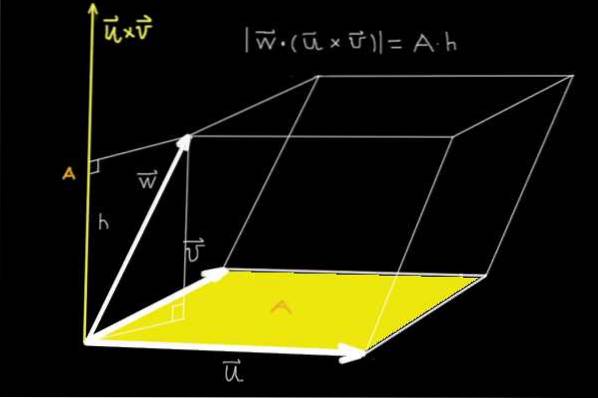
A razão é a seguinte; Quando dois dos vetores não coplanares são multiplicados vetorialmente, é obtido um vetor cuja magnitude é a área do paralelogramo que eles geram..
Então, quando esse vetor é escalarmente multiplicado pelo terceiro vetor não coplanar, o que temos é a projeção para um vetor perpendicular ao plano determinado pelos dois primeiros multiplicado pela área que eles determinam..
Ou seja, temos a área do paralelogramo gerada pelos dois primeiros multiplicada pela altura do terceiro vetor.
Condição alternativa de não coplanaridade
Se você tiver três vetores e nenhum deles puder ser escrito como uma combinação linear dos outros dois, então os três vetores são não coplanares. São três vetores ou, v Y C são não coplanares se a condição:
α ou + β v + γ C = 0
É cumprido apenas quando α = 0, β = 0 e γ = 0.
Exercícios resolvidos
-Exercício 1
Existem três vetores
ou = (-3, -6, 2); v = (4, 1, 0) e C = (-1, 2, z)
Observe que o componente z do vetor C É desconhecido.
Encontre a faixa de valores que z pode assumir de forma a garantir que os três vetores não compartilhem o mesmo plano.
Solução
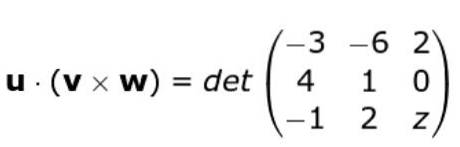
C • ( ou X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18
Nós definimos esta expressão igual ao valor zero
21 z + 18 = 0
e resolvemos para z
z = -18 / 21 = -6/7
Se a variável z assumisse o valor -6/7, os três vetores seriam coplanares.
Portanto, os valores de z que garantem que os vetores são não coplanares são aqueles no seguinte intervalo:
z ∈ (-∞, -6 / 7) U (-6/7, ∞)
-Exercício 2
Encontre o volume do paralelepípedo mostrado na figura a seguir:
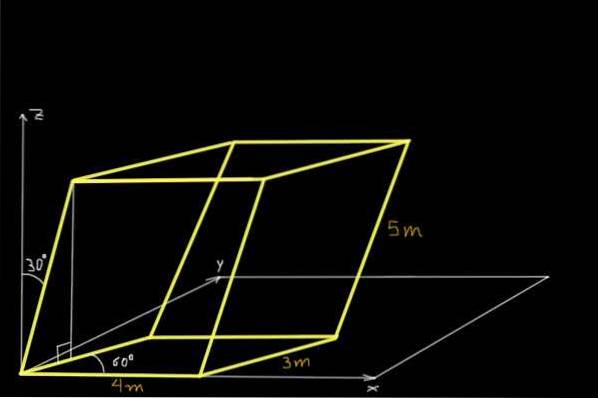
Solução
Para encontrar o volume do paralelepípedo mostrado na figura, serão determinadas as componentes cartesianas de três vetores não coplanares concorrentes na origem do sistema de coordenadas. O primeiro é o vetor ou 4m e paralelo ao eixo X:
ou= (4, 0, 0) m
O segundo é o vetor v no plano XY de tamanho 3m formando 60º com o eixo X:
v= (3 * cos 60º, 3 * sen 60º, 0) = (1,5, 2,6, 0,0) m
E o terceiro o vetor C de 5m e cuja projeção no plano XY forma 60º com o eixo X, além disso w forma 30º com o eixo Z.
C= (5 * sin 30º * cos 60º, 5 * sin 30º * sin 60º, 5 * sin 30º)
Depois de efetuados os cálculos, temos: C= (1,25, 2,17, 2,5) m.
Referências
- Figueroa, D. Série: Física para Ciências e Engenharia. Volume 1. Cinemática. 31-68.
- Fisica. Módulo 8: Vetores. Recuperado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecânica para Engenheiros. Estático. 6ª Edição. Continental Publishing Company 28-66.
- McLean, W. Schaum Series. Mecânica para Engenheiros: Estática e Dinâmica. 3ª edição. McGraw Hill. 1-15.
- Wikipedia. Vetor. Recuperado de: es.wikipedia.org


Ainda sem comentários