
Definição e fórmulas da velocidade angular média, exercícios resolvidos
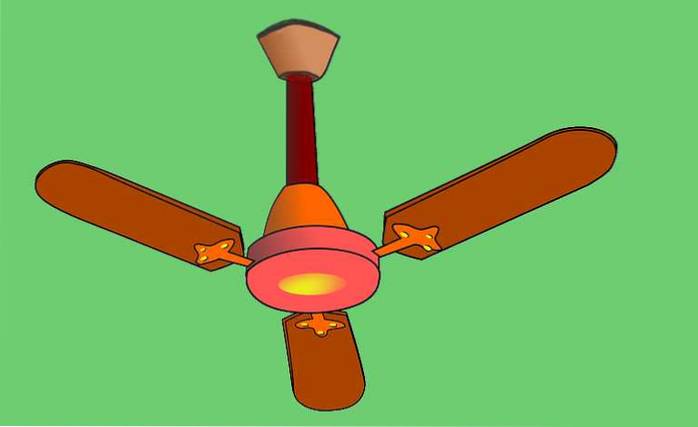
O velocidade angular média A rotação é definida como o ângulo girado por unidade de tempo do vetor de posição de um ponto que descreve o movimento circular. As pás de um ventilador de teto (como a mostrada na figura 1) seguem um movimento circular e sua velocidade angular média de rotação é calculada tomando o quociente entre o ângulo girado e o tempo em que esse ângulo foi percorrido..
As regras que o movimento rotacional segue são um tanto semelhantes às conhecidas para o movimento translacional. As distâncias percorridas também podem ser medidas em metros, porém as magnitudes angulares assumem especial relevância porque facilitam muito a descrição do movimento..
Em geral, as letras gregas são usadas para as quantidades angulares e as letras latinas para as quantidades lineares correspondentes..
Índice do artigo
- 1 Definição e fórmulas
- 1.1 Rotação uniforme
- 2 exercícios resolvidos
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Definição e fórmulas
A Figura 2 representa o movimento de um ponto em um caminho circular c. A posição P do ponto corresponde ao instante t e a posição angular correspondente a esse instante é ϕ.
A partir do instante t, decorre um período de tempo Δt. Nesse período, a nova posição do ponto é P 'e a posição angular aumentou em um ângulo Δϕ.
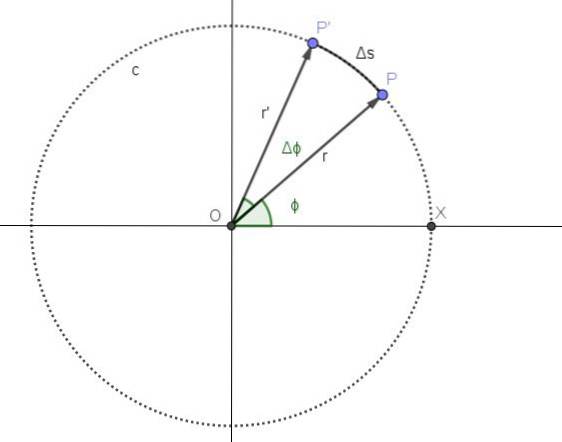
A velocidade angular média ω é o ângulo percorrido por unidade de tempo, de modo que o quociente Δϕ / Δt representará a velocidade angular média entre os tempos t e t + Δt:
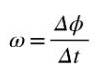
Como o ângulo é medido em radianos e o tempo em segundos, a unidade para a velocidade angular média é rad / s. Se você deseja calcular o velocidade angular bem no instante t, então teremos que calcular o quociente Δϕ / Δt quando Δt ➡0.

Rotação uniforme
Um movimento rotacional é uniforme se, em qualquer instante observado, o ângulo percorrido for o mesmo no mesmo período de tempo. Se a rotação for uniforme, então a velocidade angular em qualquer instante coincide com a velocidade angular média.
Em um movimento de rotação uniforme, o tempo em que uma revolução completa é feita é chamado de período e é denotado por T.
Além disso, quando uma volta completa é feita, o ângulo percorrido é de 2π, portanto, em uma rotação uniforme, a velocidade angular ω está relacionada ao período T, pela seguinte fórmula:
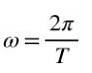
Define o frequência F de uma rotação uniforme como o quociente entre o número de voltas e o tempo utilizado para percorrê-las, ou seja, se N voltas forem feitas no período de tempo Δt então a frequência será:
f = N / Δt
Uma vez que uma curva (N = 1) é percorrida no tempo T (o período), a seguinte relação é obtida:
f = 1 / T
Ou seja, em uma rotação uniforme a velocidade angular está relacionada com a frequência através da relação:
ω = 2π ・ f
Relação entre velocidade angular e velocidade linear
Velocidade linear v, é o quociente entre a distância percorrida e o tempo gasto para percorrê-la. Na figura 2, a distância percorrida é o comprimento do arco Δs.
O arco Δs é proporcional ao ângulo percorrido Δϕ e ao raio r, sendo cumprida a seguinte relação:
Δs = r ・ Δϕ
Contanto que Δϕ seja medido em radianos.
Se dividirmos a expressão anterior pelo lapso de tempo Δt, obteremos:
(Δs / Δt) = r ・ (Δϕ / Δt)
O quociente do primeiro membro é a velocidade linear e o quociente do segundo membro é a velocidade angular média:
v = r ・ ω
Exercícios resolvidos
-Exercício 1
As pontas das pás do ventilador de teto mostradas na figura 1 movem-se com velocidade de 5 m / se as pás possuem raio de 40 cm.
Com esses dados, calcule: i) a velocidade angular média da roda, ii) o número de voltas que a roda dá em um segundo, iii) o período em segundos.
Solução
i) A velocidade linear é v = 5 m / s.
O raio é r = 0,40 m.
A partir da relação entre a velocidade linear e a velocidade angular, resolvemos para a última:
v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 voltas / s
iii) T = 1 / f = 1 / (2 volta / s) = 0,5 s para cada volta.
-Exercício 2
Um carrinho de brinquedo se move em uma pista circular com raio de 2m. Em 0s sua posição angular é 0 rad, mas após o tempo t sua posição angular é
φ (t) = 2 ・ t .
Com esses dados
i) Calcule a velocidade angular média nos seguintes intervalos de tempo [0s, 0,5s]; [0,5s, 1,0s]; [1.0s, 1.5s] e finalmente no período [0.0s, 1.5s].
ii) Com base nos resultados da parte i) O que pode ser dito sobre o movimento?
iii) Determine a velocidade linear média no mesmo período de tempo da parte i)
iv) Encontre a velocidade angular e a velocidade linear para qualquer instante.
Solução
i) A velocidade angular média é dada pela seguinte fórmula:
Passamos a calcular o ângulo percorrido e o lapso de tempo decorrido em cada intervalo.
Intervalo 1: Δϕ = ϕ (0,5s) - ϕ (0,0s) = 2 (rad / s) * 0,5s - 2 (rad / s) * 0,0s = 1,0 rad
Δt = 0,5s - 0,0s = 0,5s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Intervalo 2: Δϕ = ϕ (1,0s) - ϕ (0,5s) = 2 (rad / s) * 1,0s - 2 (rad / s) * 0,5s = 1,0 rad
Δt = 1,0s - 0,5s = 0,5s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Intervalo 3: Δϕ = ϕ (1,5s) - ϕ (1,0s) = 2 (rad / s) * 1,5s - 2 (rad / s) * 1,0s = 1,0 rad
Δt = 1,5s - 1,0s = 0,5s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Intervalo 4: Δϕ = ϕ (1,5s) - ϕ (0,0s) = 2 (rad / s) * 1,5s - 2 (rad / s) * 0,0s = 3,0 rad
Δt = 1.5s - 0.0s = 1.5s
ω = Δϕ / Δt = 3,0rad / 1,5s = 2,0 rad / s
ii) Tendo em vista os resultados anteriores, nos quais a velocidade angular média foi calculada em diferentes intervalos de tempo, obtendo-se sempre o mesmo resultado, parece indicar que se trata de um movimento circular uniforme. No entanto, esses resultados não são conclusivos..
A maneira de garantir a conclusão é calcular a velocidade angular média para um intervalo arbitrário [t, t ']: Δϕ = ϕ (t') - ϕ (t) = 2 * t '- 2 * t = 2 * (t '-t)
Δt = t '- t
ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2,0 rad / s
Isso significa que o carrinho de brinquedo tem uma velocidade angular média constante de 2 rad / s em qualquer período de tempo considerado. Mas você pode ir mais longe se calcular a velocidade angular instantânea:
Isso é interpretado como se o carrinho de brinquedo sempre tivesse velocidade angular constante = 2 rad / s.
Referências
- Giancoli, D. Physics. Princípios com aplicativos. 6ª Edição. Prentice Hall. 30-45.
- Kirkpatrick, L. 2007. Physics: A Look at the World. 6ta Edição reduzida. Cengage Learning. 117.
- Resnick, R. (1999). Fisica. Volume 1. Terceira edição em espanhol. México. Compañía Editorial Continental S.A. de C.V. 33-52.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7º. Edição. México. Editores do Cengage Learning. 32-55.
- Wikipedia. Velocidade angular. Recuperado de: wikipedia.com


Ainda sem comentários