
Velocidade areolar como é calculada e os exercícios resolvidos
O velocidade areolar é a área varrida por unidade de tempo e é constante. É específico para cada planeta e surge da descrição da segunda lei de Kepler em forma matemática. Neste artigo iremos explicar o que é e como é calculado.
O boom que representa a descoberta de planetas fora do sistema solar reanimou o interesse no movimento planetário. Nada sugere que esses exoplanetas sigam outras leis além das já conhecidas e válidas no sistema solar: as leis de Kepler..
Johannes Kepler foi o astrônomo que, sem a ajuda do telescópio e usando as observações de seu mentor Tycho Brahe, criou um modelo matemático que descreve o movimento dos planetas ao redor do Sol..
Ele deixou esse modelo consubstanciado nas três leis que levam seu nome e que permanecem tão válidas hoje quanto em 1609, quando instituiu as duas primeiras e em 1618, data em que enunciou a terceira..
Índice do artigo
- 1 Leis de Kepler
- 2 Por que os planetas se movem elipticamente em torno do Sol?
- 3 A magnitude da velocidade linear de um planeta não é constante
- 4 velocidade areolar
- 5 Calculando a velocidade linear e a velocidade areolar
- 5.1 Exercício
- 6 Bibliografia
Leis de Kepler
Na linguagem de hoje, as três leis de Kepler são assim:
1. As órbitas de todos os planetas são elípticas e o Sol está em foco.
2. O vetor de posição do Sol para um planeta varre áreas iguais em tempos iguais.
3. O quadrado do período orbital de um planeta é proporcional ao cubo do semieixo maior da elipse descrita..
Um planeta terá uma velocidade linear, assim como qualquer objeto em movimento conhecido. E mais: ao escrever a segunda lei de Kepler de forma matemática, surge um novo conceito denominado velocidade areolar, típica de cada planeta..
Por que os planetas se movem elipticamente em torno do Sol?
A Terra e os outros planetas giram em torno do Sol graças ao fato de que ele exerce uma força sobre eles: a atração gravitacional. O mesmo acontece com qualquer outra estrela e os planetas que compõem seu sistema, se os houver..
Esta é uma força do tipo conhecido como força central. O peso é uma força central com a qual todos estão familiarizados. O objeto que exerce a força central, seja o Sol ou uma estrela distante, atrai os planetas em direção ao seu centro e eles se movem em uma curva fechada.
Em princípio, essa curva pode ser aproximada como uma circunferência, como fez Nicolás Copernicus, um astrônomo polonês que criou a teoria heliocêntrica..
A força responsável é a atração gravitacional. Essa força depende diretamente das massas da estrela e do planeta em questão e é inversamente proporcional ao quadrado da distância que os separa..
O problema não é tão fácil, pois em um sistema solar, todos os elementos interagem dessa forma, agregando complexidade ao assunto. Além disso, eles não são partículas, uma vez que estrelas e planetas têm tamanhos mensuráveis..
Por esse motivo, o ponto central da órbita ou circuito percorrido pelos planetas não está exatamente centrado na estrela, mas em um ponto conhecido como centro de gravidade do sistema planeta sol..
A órbita resultante é elíptica. A imagem a seguir mostra isso, tomando a Terra e o Sol como exemplo:
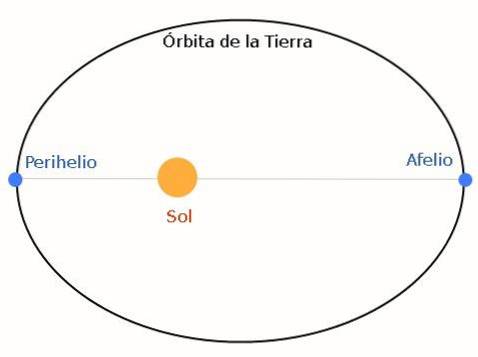
O afélio é a posição mais distante do Sol na Terra, enquanto o periélio é o ponto mais próximo. A elipse pode ser mais ou menos achatada, dependendo das características do sistema planeta estrela..
Os valores do afélio e do periélio variam anualmente, pois os outros planetas causam distúrbios. Para outros planetas, essas posições são chamadas de apoaster e periaster, respectivamente..
A magnitude da velocidade linear de um planeta não é constante
Kepler descobriu que quando um planeta orbita o Sol, durante seu movimento ele varre áreas iguais em tempos iguais. A Figura 2 mostra graficamente o significado disso:
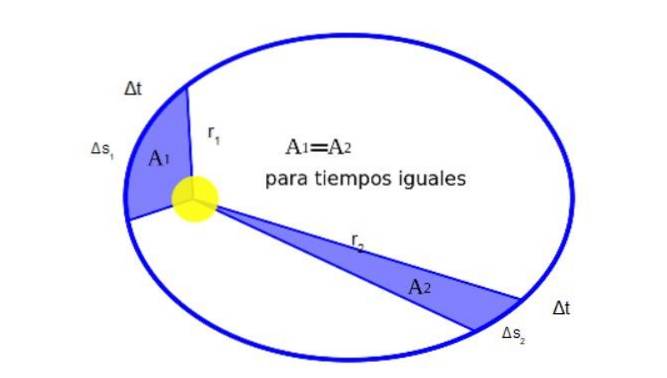
Matematicamente, o fato de que A1 ser igual a Adois é expresso assim:

Os arcos percorridos Δs são pequenos, de modo que cada área pode se aproximar da de um triângulo:
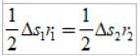
Uma vez que Δs =vΔt, onde v é a velocidade linear do planeta em um determinado ponto, ao substituir temos:
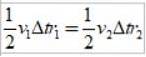
E como o intervalo de tempo Δt é o mesmo, obtemos:
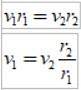
Como rdois > r1, então v1 > vdois, em outras palavras, a velocidade linear de um planeta não é constante. Na verdade, a Terra se move mais rápido quando está no periélio do que quando está no afélio..
Portanto a velocidade linear da Terra ou de qualquer planeta ao redor do Sol não é uma magnitude que sirva para caracterizar o movimento desse planeta..
Velocidade areolar
A segunda lei de Kepler sugere uma nova magnitude chamada velocidade areolar. É definida como a área varrida por unidade de tempo e é constante. Para calculá-lo, a seguinte figura é usada:
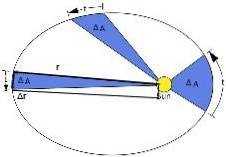
Uma pequena área varrida pela Terra é escolhida ao fazer seu circuito elíptico, que denotaremos como ΔA. O tempo necessário para isso é Δt.
A Figura 3 mostra o vetor posição da Terra em relação ao Sol, denotado por r. Quando a Terra se move, ela experimenta um deslocamento Δr.
Esta área corresponde a metade da área do retângulo mostrado na figura 3:
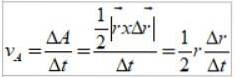
O quociente Δr / Δt é precisamente a velocidade linear da Terra, então a velocidade areolar é como:
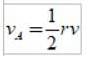
As unidades de vPARA no Sistema Internacional são:
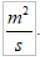
Observe que, embora r e v variem, o produto permanece constante. Isso torna a velocidade areolar uma magnitude muito adequada para caracterizar o movimento de um planeta em torno de sua estrela..
O produto de rev é a magnitude do momento angular L, de modo que a velocidade areolar pode ser expressa como:
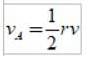
Calculando a velocidade linear e velocidade areolar
Com o exemplo a seguir, mostraremos como calcular a velocidade areolar quando alguns parâmetros do movimento planetário são conhecidos:
Exercício
Um exoplaneta se move ao redor de seu Sol seguindo uma órbita elíptica, de acordo com as leis de Kepler. Quando está no periastro, seu vetor de raio é r1 = 4 107 km, e quando está em apoastro é rdois = 15 107 km. A velocidade linear em seu periastro é v1 = 1000 km / s.
Calcular:
A) A magnitude da velocidade no apoastro.
B) A velocidade areolar do exo-planeta.
C) O comprimento do semieixo maior da elipse.
Responda para)
A equação é usada:
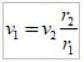
em que os valores numéricos são substituídos.
Cada termo é identificado da seguinte forma:
v1 = velocidade em apoastro; vdois = velocidade no periastro; r1= distância de apoastro,
rdois= distância do periastro.
Com esses valores você obtém:

Resposta B)
A equação a usar é
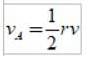
em que o par de valores rev do periastro ou do apoastro pode ser substituído, uma vez que vPARA é uma constante do planeta:

Resposta C)
O comprimento do semieixo maior da elipse é o semisum do apoastro e do periastro:
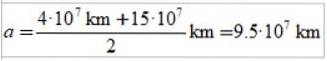
Bibliografia
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. México. Editores do Cengage Learning. 367-372.
- Stern, D. (2005). As Três Leis do Movimento Planetário de Kepler. Recuperado de pwg.gsfc.nasa.gov
- Observação: o exercício proposto foi feito e modificado a partir do texto a seguir em um livro da McGrawHill. Infelizmente, é um capítulo isolado em formato pdf, sem título ou autor: mheducation.es/bcv/guide/capitulo/844817027X.pdf



Ainda sem comentários