
Definição instantânea de velocidade, fórmula, cálculo e exercícios
O velocidade instantânea é definido como a mudança instantânea do deslocamento no tempo. É um conceito que adiciona grande precisão ao estudo do movimento. E é um avanço com relação à velocidade média, cujas informações são muito gerais.
Para obter a velocidade instantânea, vamos examinar o menor intervalo de tempo possível. O cálculo diferencial é a ferramenta perfeita para expressar essa ideia matematicamente.

O ponto de partida é a velocidade média:

Esse limite é conhecido como derivado. Na notação de cálculo diferencial, temos:
))
Sempre que o movimento é restrito a uma linha reta, a notação vetorial pode ser dispensada.
Índice do artigo
- 1 Cálculo da velocidade instantânea: interpretação geométrica
- 2 Alguns casos especiais no cálculo da velocidade instantânea
- 3 exercícios resolvidos de velocidade instantânea
- 3.1 Exercício 1
- 3.2 Exercício 2
- 4 referências
Cálculo da velocidade instantânea: interpretação geométrica
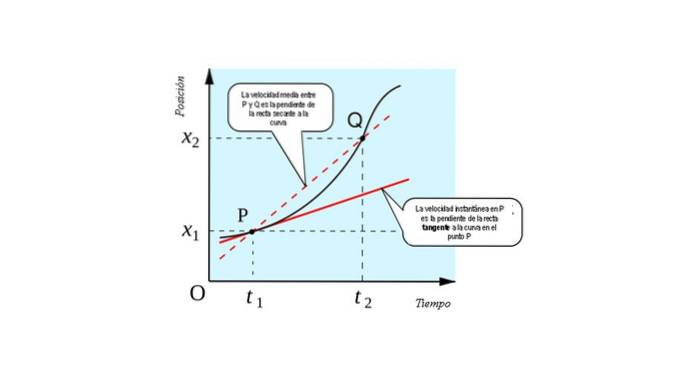
A figura a seguir mostra a interpretação geométrica do conceito de derivada: é a inclinação da reta tangente para a curva x (t) vs. t em cada ponto.

Você pode imaginar como obter o limite se o ponto Q for se aproximando aos poucos do ponto P. Chegará o momento em que os dois pontos estarão tão próximos que você não conseguirá distinguir um do outro..
A linha que os une passará de secante (linha que cruza em dois pontos) a tangente (linha que toca a curva em apenas um ponto). Portanto, para encontrar a velocidade instantânea de uma partícula em movimento, devemos ter:
- O gráfico da posição da partícula em função do tempo. Encontrando a inclinação da reta tangente à curva a cada instante do tempo, temos a velocidade instantânea em cada ponto que a partícula ocupa.
O bem:
- A função de posição de partícula x (t), que é derivado para obter a função de velocidade v (t), então esta função é avaliada em cada batida t, na conveniência. A função de posição é considerada diferenciável.
Alguns casos especiais no cálculo da velocidade instantânea
-A inclinação da linha tangente à curva em P é 0. Uma inclinação zero significa que o móvel está estacionário e que sua velocidade é, naturalmente, 0.
-A inclinação da reta tangente à curva em P é maior que 0. A velocidade é positiva. No gráfico acima, significa que o celular está se afastando de O.
-A inclinação da linha tangente à curva em P é menor que 0. A velocidade seria negativa. No gráfico acima não existem tais pontos, mas neste caso a partícula estaria se aproximando de O.
-A inclinação da linha tangente à curva é constante em P e em todos os outros pontos. Neste caso, o gráfico é uma linha reta e o celular tem movimento de linha uniforme MRU (sua velocidade é constante).
Em geral, a função v (t) é também uma função do tempo, que por sua vez pode ter uma derivada. E se não fosse possível encontrar as derivadas das funções x (t) Y v (t)?
Em caso de x (t) pode ser que a inclinação - a velocidade instantânea - mude de sinal abruptamente. Ou que iria de zero para um valor diferente imediatamente.
Se sim, o gráfico x (t) apresentaria pontos ou cantos nos locais de mudanças repentinas. Muito diferente do caso representado na imagem anterior, em que a curva x (t) é uma curva suave, sem pontos, cantos, descontinuidades ou mudanças abruptas.
A verdade é que para celulares reais, as curvas suaves são as que melhor representam o comportamento do objeto.
O movimento em geral é bastante complexo. Os móbiles podem ser parados por um tempo, acelerar para ir do repouso para ter uma velocidade e se afastar do ponto inicial, manter a velocidade por um tempo, então frear para parar novamente e assim por diante..
Novamente, eles podem começar de novo e continuar na mesma direção. Ou acione o reverso e volte. Isso é chamado de movimento variado em uma dimensão..
Aqui estão alguns exemplos de cálculo da velocidade instantânea para esclarecer o uso das definições fornecidas:
Exercícios resolvidos de velocidade instantânea
Exercício 1
Uma partícula se move ao longo de uma linha reta com a seguinte lei do movimento:
x (t) = -t3 + 2 tdois + 6 t - 10
Todas as unidades estão no Sistema Internacional. Achar:
a) A posição da partícula em t = 3 segundos.
b) A velocidade média no intervalo entre t = 0 se t = 3 s.
c) A velocidade média no intervalo entre t = 0 se t = 3 s.
d) A velocidade instantânea da partícula da questão anterior, em t = 1 s.
Respostas
a) Para encontrar a posição da partícula, a lei do movimento (função posição) é avaliada em t = 3:
x (3) = (-4/3) .33 + 2,3dois + 6,3 - 10 m = -10 m
Não há problema que a posição seja negativa. O sinal (-) indica que a partícula está à esquerda da origem O.
b) No cálculo da velocidade média, são necessárias as posições final e inicial da partícula nos tempos indicados: x (3) e x (0). A posição em t = 3 é x (3) e é conhecida pelo resultado anterior. A posição em t = 0 segundos é x (0) = -10 m.
Como a posição final é igual à posição inicial, conclui-se imediatamente que a velocidade média é 0.
c) A velocidade média é a relação entre a distância percorrida e o tempo gasto. Agora, a distância é o módulo ou magnitude do deslocamento, portanto:
distância = | x2 - x1 | = | -10 - (-10) | m = 20 m
Observe que a distância percorrida é sempre positiva.
vm = 20 m / 3 s = 6,7 m / s
d) Aqui é necessário encontrar a primeira derivada da posição em relação ao tempo. Em seguida, é avaliado por t = 1 segundo.
x '(t) = -4 tdois + 4 t + 6
x '(1) = -4,1dois + 4,1 + 6 m / s = 6 m / s
Exercício 2
Abaixo está o gráfico da posição de um celular em função do tempo. Encontre a velocidade instantânea em t = 2 segundos.
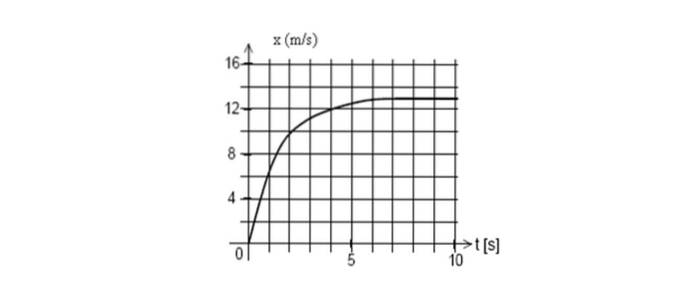
Responder
Desenhe a linha tangente à curva em t = 2 segundos e, em seguida, calcule sua inclinação, tomando quaisquer dois pontos na linha.
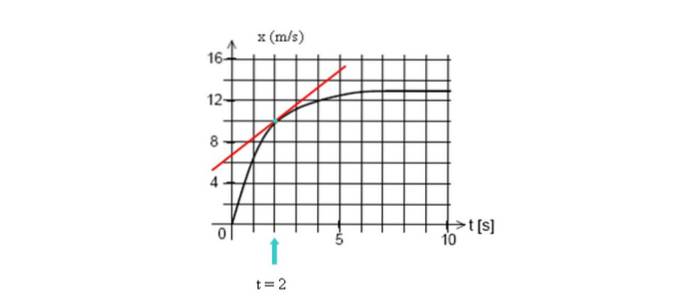
Neste exemplo vamos tomar dois pontos de fácil visualização, cujas coordenadas são (2 s, 10 m) e o corte com o eixo vertical (0 s, 7 m):

Referências
- Giancoli, D. Física. Princípios com aplicativos. 6º Edição. Prentice Hall. 22-25.
- Resnick, R. (1999). Fisica. Volume 1. Terceira edição em espanhol. México. Compañía Editorial Continental S.A. de C.V. 21-22.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7mãe. Edição. México. Editores do Cengage Learning. 23-25.



Ainda sem comentários